c4dynamics.states.lib.rigidbody.rigidbody.inteqm

rigidbody.inteqm(forces, moments, dt)

Advances the state vector, rigidbody.X, with respect to the input forces and moments on a single step of time, dt.

Integrates equations of six degrees motion using the Runge-Kutta method.

This method numerically integrates the equations of motion for a dynamic system using the fourth-order Runge-Kutta method as given by eqm.int6.

The derivatives of the equations are of six dimensional motion as given by eqm.eqm6.

Parameters:

• forces (numpy.array or list) – An external forces vector acting on the body, forces = [Fx, Fy, Fz]

• moments (numpy.array or list) – An external moments vector acting on the body, moments = [Mx, My, Mz]

• dt (float or int) – Interval time step for integration.

Returns:

out (numpy.float64) – An acceleration array at the final time step.

Warning

This method is not recommanded when the vectors of forces or moments depend on the state variables. Since the vectors of forces and moments are provided once at the entrance to the integration, they remain constant for the entire steps. Therefore, when the forces or moments depend on the state variables the results of this method are not accurate and may lead to instability.

Examples

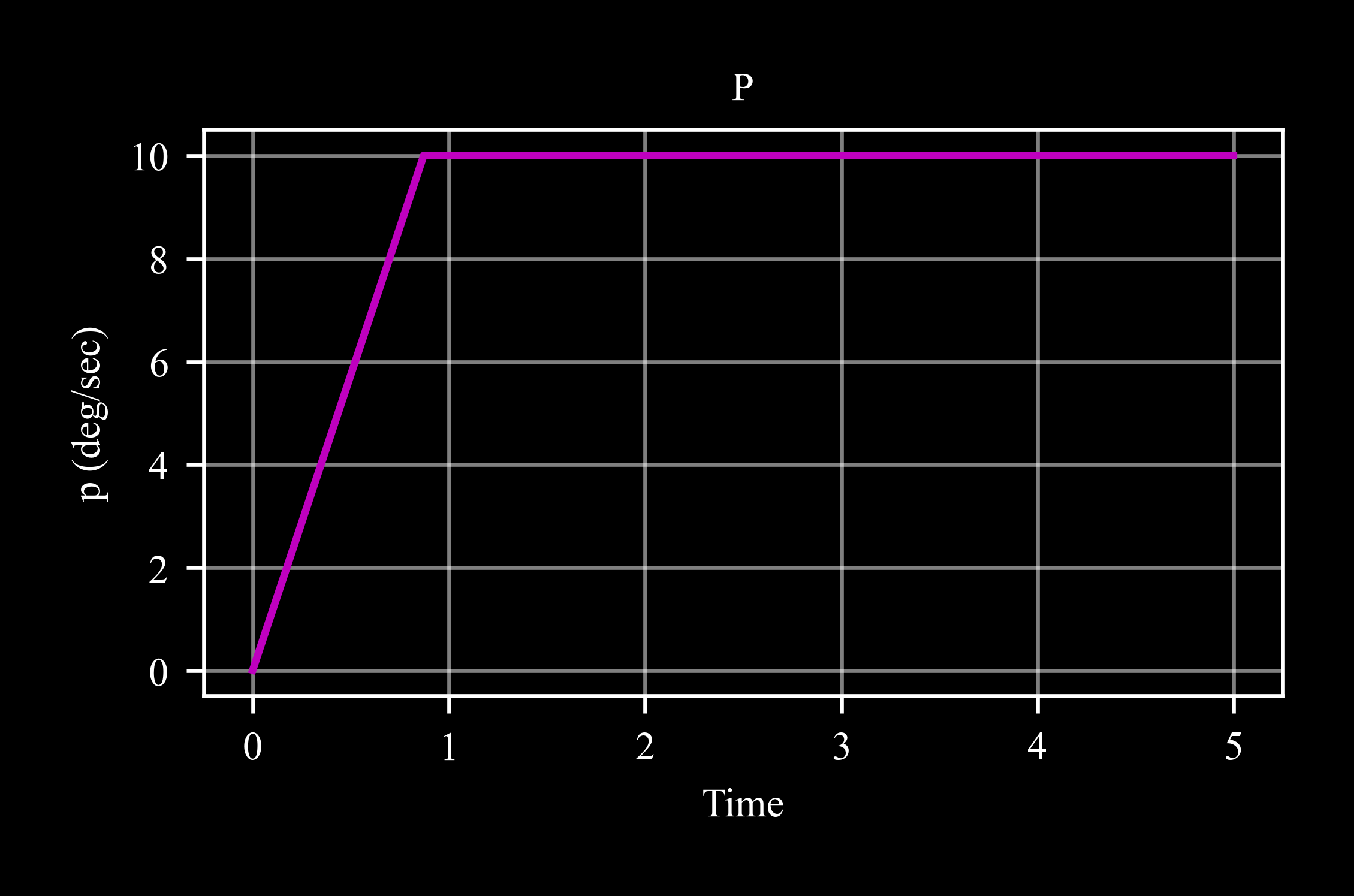
A torque is applied by spacecraft thrusters to stabilize the roll in a constant rate.

Import required packages:

>>> import c4dynamics as c4d
>>> from matplotlib import pyplot as plt
>>> import numpy as np

Settings and initial conditions:

>>> dt = 0.001
>>> torque = [0.1, 0, 0]
>>> rb = c4d.rigidbody()
>>> rb.I = [0.5, 0, 0]  # Moment of inertia about x

Main loop:

>>> for ti in np.arange(0, 5, dt):
...   rb.inteqm(np.zeros(3), torque, dt)  
...   if rb.p >= 10 * c4d.d2r:
...     torque = [0, 0, 0]
...   rb.store(ti)

Plot results:

>>> rb.plot('p')
>>> plt.show()