Seeker

Contents

Seeker#

class c4dynamics.sensors.seeker.seeker(origin: rigidbody | None = None, isideal: bool = False, **kwargs)[source]#

Direction seeker.

The seeker class models sensors that measure the direction to a target in terms of azimuth and elevation. Such sensors typically use electro-optical or laser technologies, though other technologies may also be used.

A seeker object can operate in an ideal mode, providing precise direction measurements. Alternatively, in a non-ideal mode, the measurements may be affected by errors such as scale factor, bias, and noise, as defined by the errors model. A random variable generation mechanism allows for Monte Carlo simulations.

Parameters:

  • origin (rigidbody, optional) – A rigidbody object whose state vector X determines the seeker’s initial position and attitude. Defaults: a rigidbody object with zeros vector, X = numpy.zeros(12).

  • isideal (bool, optional) – A flag indicating whether the errors model is off. Defaults False.

Keyword Arguments:

  • bias_std (float) – The standard deviation of the bias error, [radians]. Defaults \(0.1°\).

  • scale_factor_std (float) – The standard deviation of the scale factor error, [dimensionless]. Defaults \(0.05 (= 5\%)\).

  • noise_std (float) – The standard deviation of the seeker angular noise, [radians]. Default value for non-ideal seeker: \(0.4°\).

  • dt (float) – The time-constant of the operational rate of the seeker (below which the seeker measures return None), [seconds]. Default value: \(dt = -1sec\) (no limit between calls to measure).

See also

filters, eqm, radar

Functionality

At each sample the seeker returns measures based on the true geometry with the target.

Let the relative coordinates in an arbitrary frame of reference:

\[ \begin{align}\begin{aligned}dx = target.x - seeker.x\\dy = target.y - seeker.y\\dz = target.z - seeker.z\end{aligned}\end{align} \]

The relative coordinates in the seeker body frame are given by:

\[x_b = [BR] \cdot [dx, dy, dz]^T\]

where \([BR]\) is a Body from Reference DCM (Direction Cosine Matrix) formed by the seeker three Euler angles. See the rigidbody section below.

The azimuth and elevation measures are then the spatial angles:

\[ \begin{align}\begin{aligned}az = tan^{-1}{x_b[1] \over x_b[0]}\\el = tan^{-1}{x_b[2] \over \sqrt{x_b[0]^2 + x_b[1]^2}}\end{aligned}\end{align} \]

Where:

  • \(az\) is the azimuth angle

  • \(el\) is the elevation angle

  • \(x_b\) is the target-radar position vector in radar body frame

../_images/skr_definitions.svg

Fig-1: Azimuth and elevation angles definition#

Errors Model

The azimuth and elevation angles are subject to errors: scale factor, bias, and noise.

  • Bias: represents a constant offset or deviation from the true value in the seeker’s measurements. It is a systematic error that consistently affects the measured values. The bias of a seeker instance is a normally distributed variable with mean = 0 and std = bias_std, where bias_std is a parameter with default value of 0.1°.

  • Scale Factor: a multiplier applied to the true value of a measurement. It represents a scaling error in the measurements made by the seeker. The scale factor of a seeker instance is a normally distributed variable with mean = 0 and std = scale_factor_std, , where scale_factor_std is a parameter with default value of 0.05.

  • Noise: represents random variations or fluctuations in the measurements that are not systematic. The noise at each seeker sample (measure) is a normally distributed variable with mean = 0 and std = noise_std, where noise_std is a parameter with default value of 0.4°.

The errors model generates random variables for each seeker instance, allowing for the simulation of different scenarios or variations in the seeker behavior in a technique known as Monte Carlo. Monte Carlo simulations leverage this randomness to statistically analyze the impact of these biases and scale factors over a large number of iterations, providing insights into potential outcomes and system reliability.

The errors model can be disabled by applying isideal = True at the seeker construction stage.

The erros model operates as follows: the particular parameters that form each error, for example the standard deviation of the bias error, may be determined at the stage of creating the sensor object: seeker = c4d.sensors.seeker(bias_std = 0.1 * c4d.d2r), where c4d.d2r is a conversion from degrees to radians. Then, the errors model generates a normal random variable and establishes the seeker bias error. However, the user can override the generated bias by using the bias property and determine the seeker bias error: seeker.bias = 1 * c4d.d2r, to have a 1° bias error.

rigidbody

The seeker class is a subclass of rigidbody, i.e. it suggests attributes of position and attitude and the manipulation of them.

As a fundamental propety, the rigidbody’s state vector X sets the spatial coordinates of the seeker:

\[X = [x, y, z, v_x, v_y, v_z, {\varphi}, {\theta}, {\psi}, p, q, r]^T\]

The first six coordinates determine the translational position and velocity of the seeker while the last six determine its angular attitude in terms of Euler angles and the body rates.

Passing a rigidbody parameter as an origin sets the initial conditions of the seeker.

Construction

A seeker instance is created by making a direct call to the seeker constructor:

>>> skr = c4d.sensors.seeker()

Initialization of the instance does not require any mandatory arguments, but the seeker parameters can be determined using the **kwargs argument as detailed above.

Examples

Import required packages:

>>> import c4dynamics as c4d
>>> from matplotlib import pyplot as plt
>>> import numpy as np

Target

For the examples below let’s generate the trajectory of a target with constant velocity:

>>> tgt = c4d.datapoint(x = 1000, y = 0, vx = -80 * c4d.kmh2ms, vy = 10 * c4d.kmh2ms)
>>> for t in np.arange(0, 60, 0.01):
...   tgt.inteqm(np.zeros(3), .01) 
...   tgt.store(t)

The method inteqm of the datapoint class integrates the 3 degrees of freedom equations of motion with respect to the input force vector (np.zeros(3) here).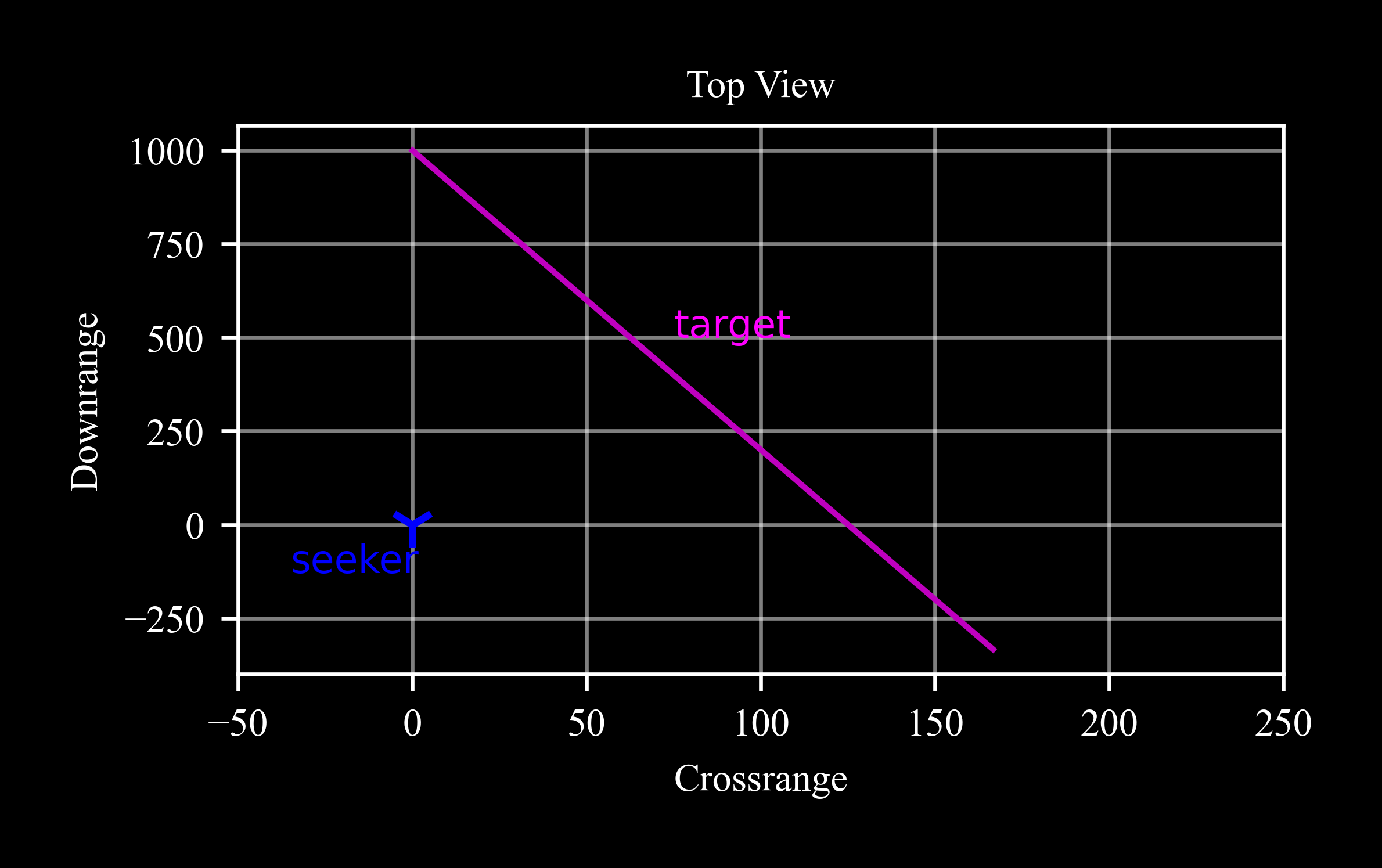

../_images/target1.png

Since the call to measure requires a target as a datapoint object we utilize a custom create function that returns a new datapoint object for a given X state vector in time.

  • c4d.kmh2ms converts kilometers per hour to meters per second.

  • c4d.r2d converts radians to degrees.

  • c4d.d2r converts degrees to radians.

Origin

Let’s also introduce a pedestal as an origin for the seeker. The pedestal is a rigidbody object with position and attitude:

>>> pedestal = c4d.rigidbody(z = 30, theta = -1 * c4d.d2r)

Ideal Seeker

Measure the target position with an ideal seeker:

>>> skr_ideal = c4d.sensors.seeker(origin = pedestal, isideal = True)
>>> for x in tgt.data():
...   skr_ideal.measure(c4d.create(x[1:]), t = x[0], store = True)

Comparing the seeker measurements with the true target angles requires converting the relative position to the seeker body frame:

>>> dx = tgt.data('x')[1] - skr_ideal.x
>>> dy = tgt.data('y')[1] - skr_ideal.y
>>> dz = tgt.data('z')[1] - skr_ideal.z
>>> Xb = np.array([skr_ideal.BR @ [X[1] - skr_ideal.x, X[2] - skr_ideal.y, X[3] - skr_ideal.z] for X in tgt.data()])

where skr_ideal.BR is a Body from Reference DCM (Direction Cosine Matrix) formed by the seeker three Euler angles

Now az_true is the true target azimuth angle with respect to the seeker, and el_true is the true elevation angle (atan2d is an aliasing of numpy’s arctan2 with a modification returning the angles in degrees):

>>> az_true = c4d.atan2d(Xb[:, 1], Xb[:, 0])
>>> el_true = c4d.atan2d(Xb[:, 2], c4d.sqrt(Xb[:, 0]**2 + Xb[:, 1]**2))
>>> # plot results
>>> fig, axs = plt.subplots(2, 1)  
>>> axs[0].plot(tgt.data('t'), az_true, label = 'target')  
>>> axs[0].plot(*skr_ideal.data('az', scale = c4d.r2d), label = 'seeker')  
>>> axs[1].plot(tgt.data('t'), el_true)  
>>> axs[1].plot(*skr_ideal.data('el', scale = c4d.r2d))
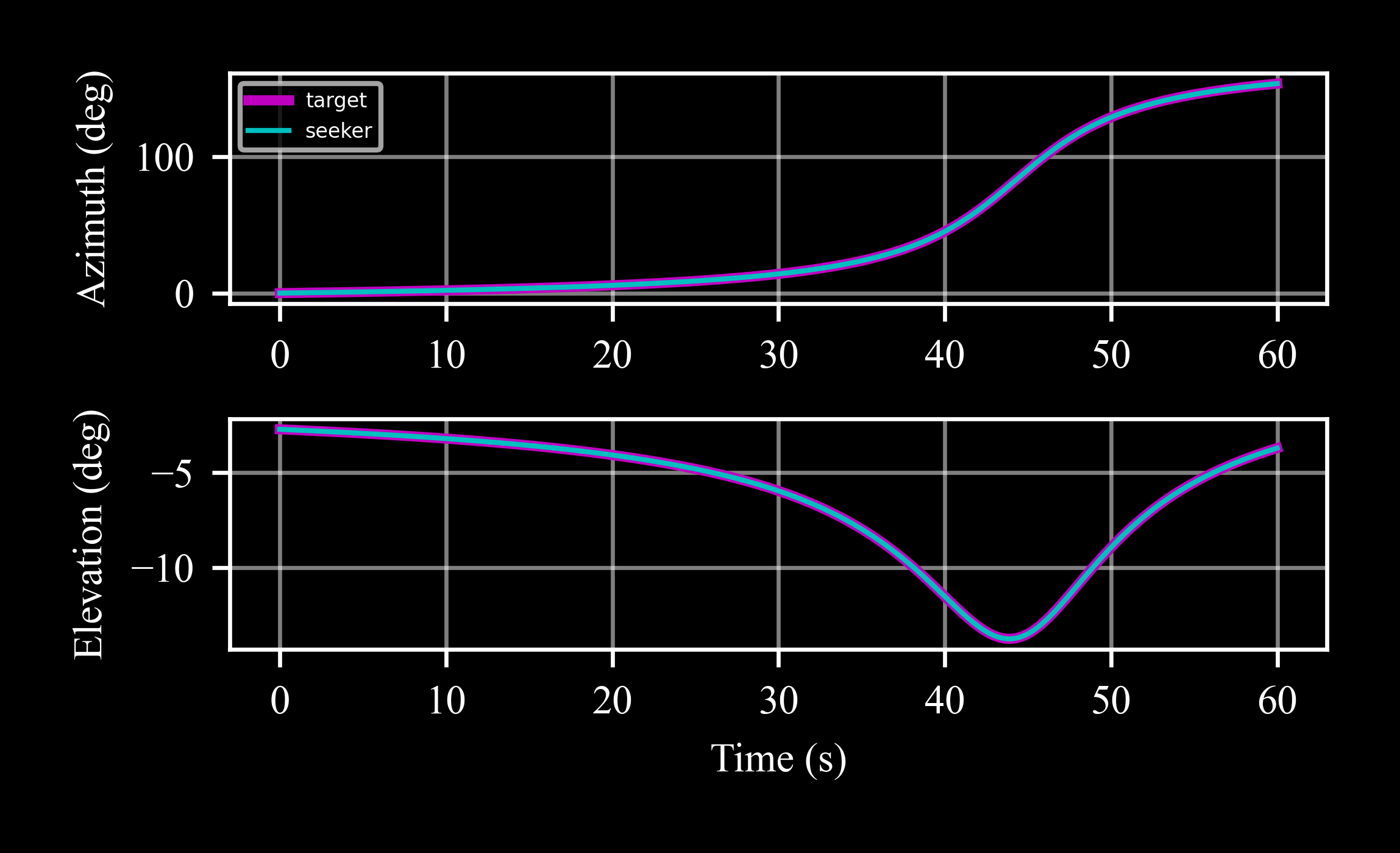
../_images/ideal1.png

Non-ideal Seeker

Measure the target position with a non-ideal seeker. The seeker’s errors model introduces bias, scale factor, and noise that corrupt the measurements.

To reproduce the result, let’s set the random generator seed (42 is arbitrary):

>>> np.random.seed(42)

>>> skr = c4d.sensors.seeker(origin = pedestal)
>>> for x in tgt.data():
...   skr.measure(c4d.create(x[1:]), t = x[0], store = True)

Results with respect to an ideal seeker:

>>> fig, axs = plt.subplots(2, 1)
>>> axs[0].plot(*skr_ideal.data('az', scale = c4d.r2d), label = 'ideal')  
>>> axs[0].plot(*skr.data('az', scale = c4d.r2d), label = 'non-ideal')  
>>> axs[1].plot(*skr_ideal.data('el', scale = c4d.r2d))  
>>> axs[1].plot(*skr.data('el', scale = c4d.r2d))
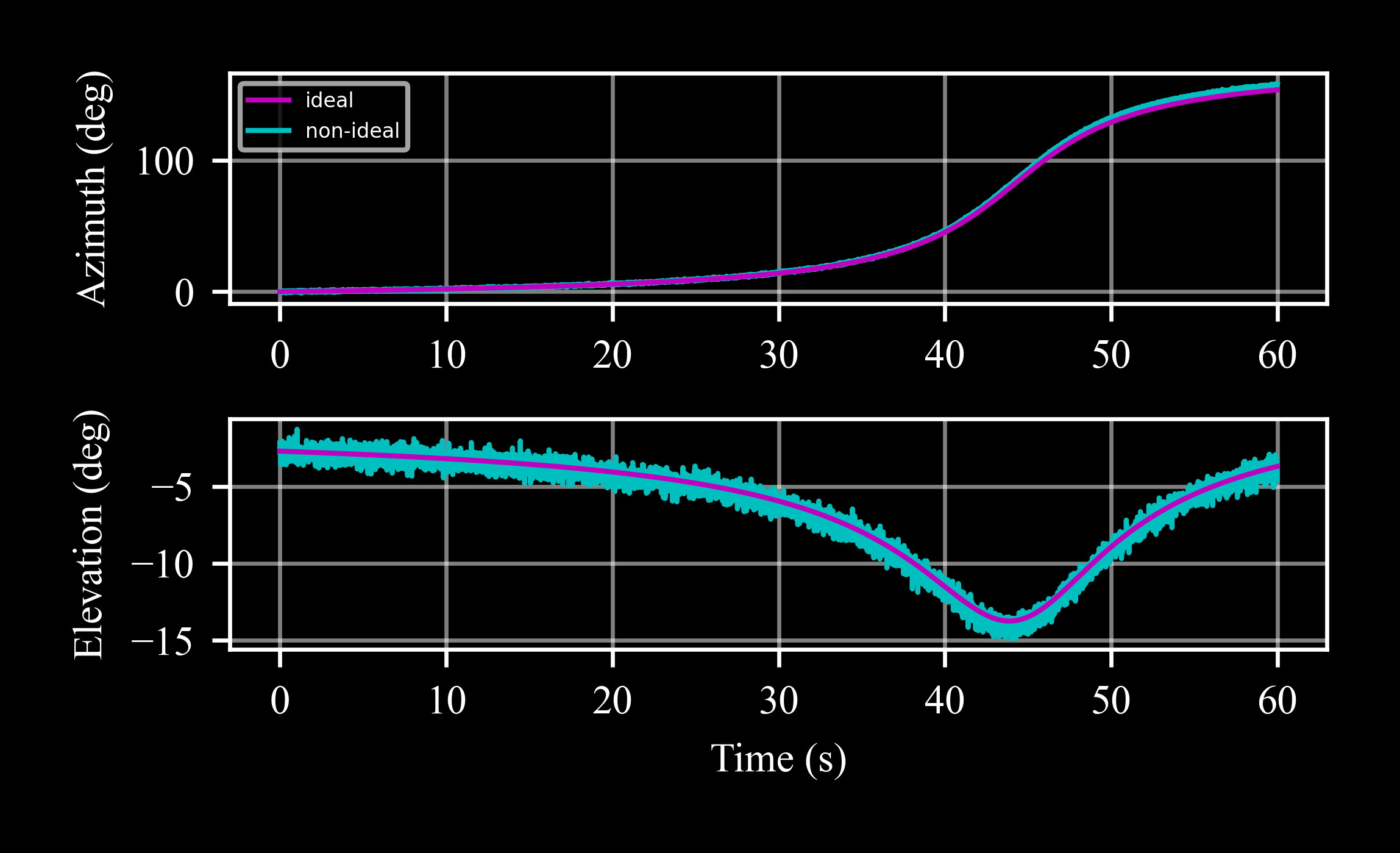
../_images/nonideal1.png

The bias, scale factor, and noise that used to generate these measures can be examined by:

>>> skr.bias * c4d.r2d 
-0.01...
>>> skr.scale_factor 
1.02...
>>> skr.noise_std * c4d.r2d
0.4

Points to consider:

  • The scale factor error increases with the angle, such that for a \(5%\) scale factor, the error of \(Azimuth = 100°\) is \(5°\), whereas the error for \(Elevation = -15°\) is only \(-0.75°\).

  • The standard deviation of the noise in the two channels is the same. However, as the Elevation values are confined to a smaller range, the effect appears more pronounced there.

Rotating Seeker

Measure the target position with a rotating seeker. The seeker origin is yawing (performed by the increment of \(\psi\)) in the direction of the target motion:

>>> skr = c4d.sensors.seeker(origin = pedestal)
>>> for x in tgt.data():
...   skr.psi += .02 * c4d.d2r
...   skr.measure(c4d.create(x[1:]), t = x[0], store = True) 
...   skr.store(x[0])

The seeker yaw angle:

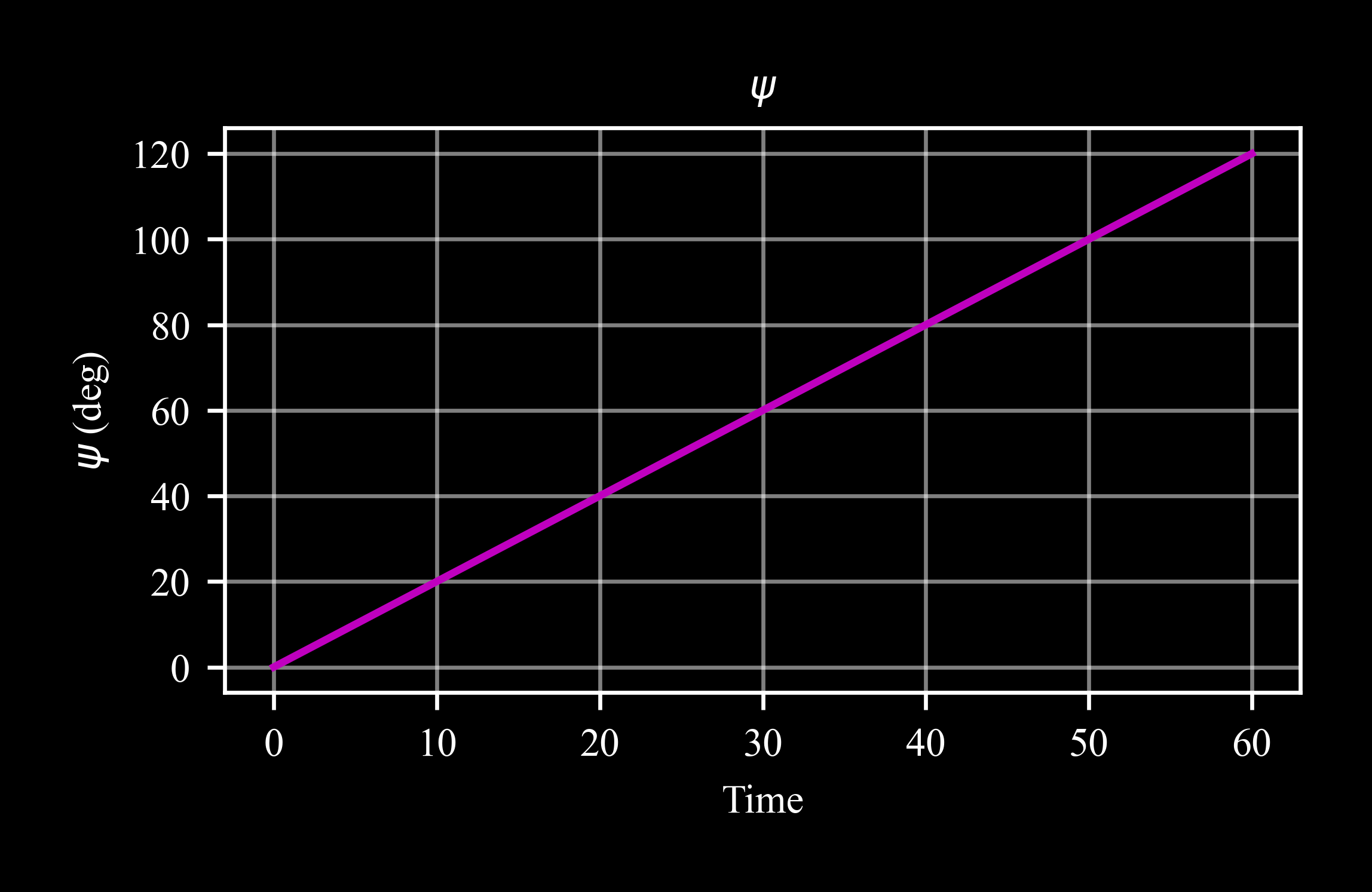
../_images/psi1.png

And the target angles with respect to the yawing seeker are:

>>> fig, axs = plt.subplots(2, 1)
>>> axs[0].plot(*skr_ideal.data('az', c4d.r2d), label = 'ideal static seeker')  
>>> axs[0].plot(*skr.data('az', c4d.r2d), label = 'non-ideal yawing seeker')  
>>> axs[1].plot(*skr_ideal.data('el', scale = c4d.r2d))  
>>> axs[1].plot(*skr.data('el', scale = c4d.r2d))
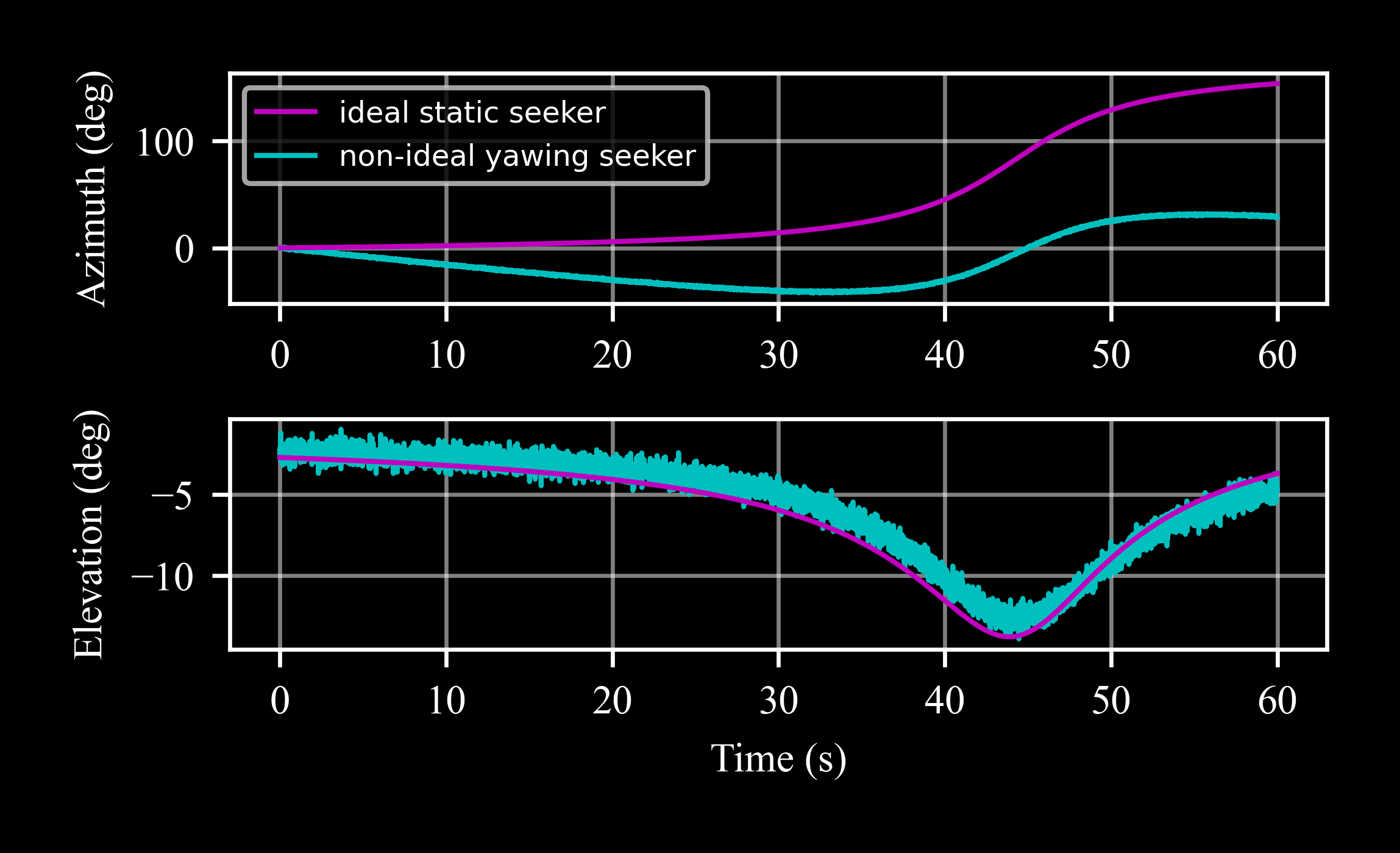
../_images/yawing1.png

  • The rotation of the seeker with the target direction keeps the azimuth angle limited, such that non-rotating seekers with limited FOV (field of view) would have lost the target.

Operation Time

By default, the seeker returns measurments for each call to measure. However, setting the parameter dt to a positive number makes measure return None for any t < last_t + dt, where t is the current measure time, last_t is the last measurement time, and dt is the seeker time-constant:

>>> np.random.seed(770)
>>> tgt = c4d.datapoint(x = 100, y = 100)
>>> skr = c4d.sensors.seeker(dt = 0.01)
>>> for t in np.arange(0, .025, .005):  
...   print(f'{t}: {skr.measure(tgt, t = t)}')
0.0: (0.73..., 0.007...)
0.005: (None, None)
0.01: (0.73..., 0.0006...)
0.015: (None, None)
0.02: (0.71..., 0.006...)

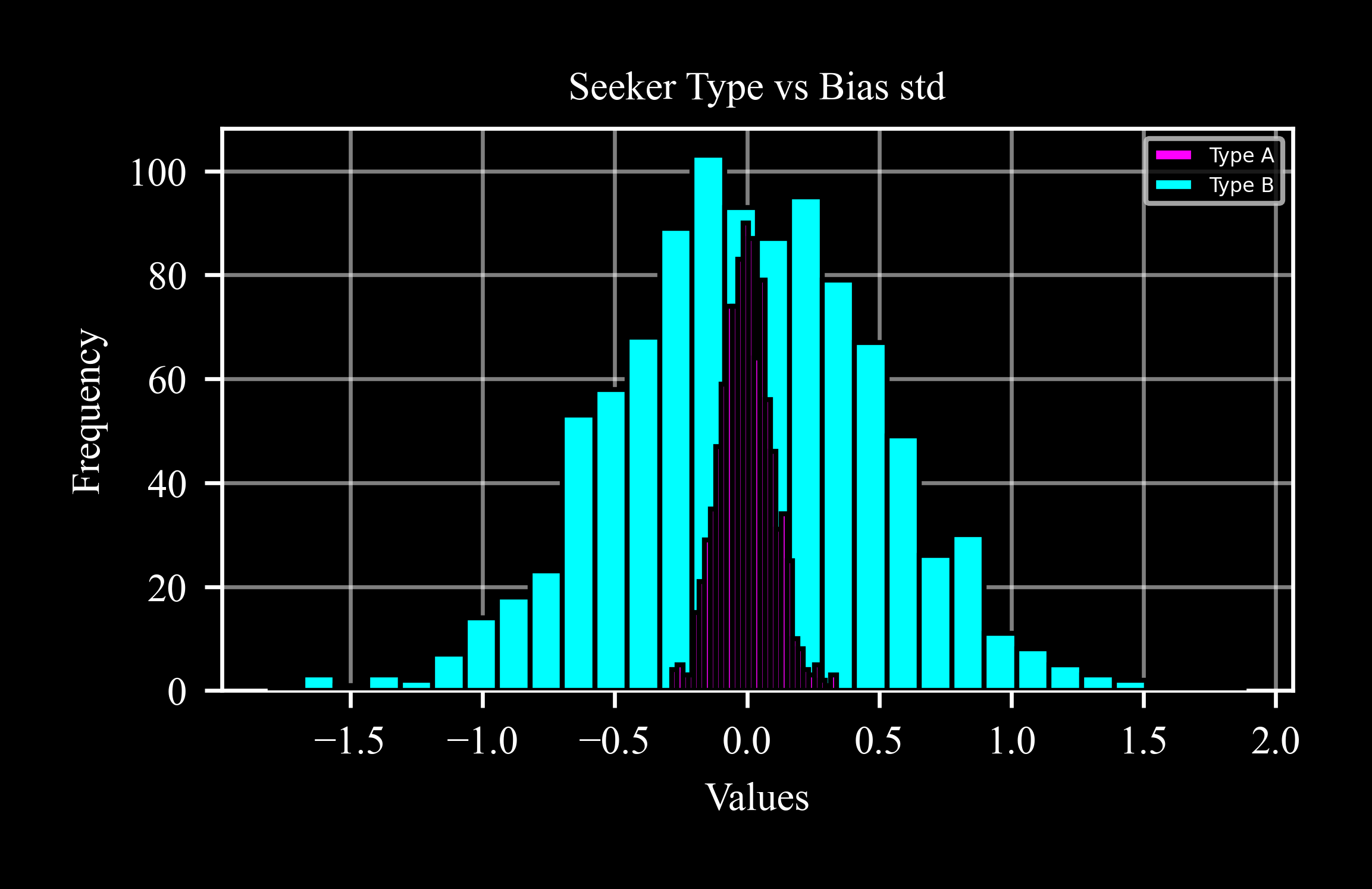
Random Distribution

The distribution of normally generated random variables across mutliple seeker instances is shown for biases of two groups of seekers:

  • One group generated with a default bias_std of 0.1°.

  • The second group with bias_std of 0.5°.

>>> from c4dynamics.sensors import seeker
>>> seekers_type_A = []
>>> seekers_type_B = []
>>> B_std = 0.5 * c4d.d2r
>>> for i in range(1000):
...   seekers_type_A.append(seeker().bias * c4d.r2d)
...   seekers_type_B.append(seeker(bias_std = B_std).bias * c4d.r2d)

The histogram highlights the broadening of the distribution as the standard deviation increases:

>>> ax = plt.subplot()
>>> ax.hist(seekers_type_A, 30, label = 'Type A')  
>>> ax.hist(seekers_type_B, 30, label = 'Type B')
../_images/bias21.png

Properties

seeker.bias

Gets and sets the object's bias.

seeker.scale_factor

Gets and sets the object's scale_factor.

Methods

seeker.measure(target[, t, store])

Measures azimuth and elevation between the seeker and a target.
Contents