c4dynamics.sensors.seeker.seeker.measure

seeker.measure(target: state, t: float = -1, store: bool = False) → tuple[float | None, float | None]

Measures azimuth and elevation between the seeker and a target.

If the seeker time-constant dt was provided when the seeker was created, then measure returns None for any t < last_t + dt, where t is the time input, last_t is the last measurement time, and dt is the seeker time-constant. Default behavior, returns measurements for each call.

If store = True, the method stores the measured azimuth and elevation along with a timestamp (t = -1 by default, if not provided otherwise).

Parameters:

• target (state) – A Cartesian state object to measure by the seeker, including at least one position coordinate (x, y, z).

• store (bool, optional) – A flag indicating whether to store the measured values. Defaults False.

• t (float, optional) – Timestamp [seconds]. Defaults -1.

Returns:

out (tuple) – azimuth and elevation, [radians].

Raises:

ValueError – If target doesn’t include any position coordinate (x, y, z).

Example

measure in a program simulating real-time tracking of a constant velcoity target.

The target is represented by a datapoint and is simulated using the eqm module, which integrating the point-mass equations of motion.

An ideal seeker uses as reference to the true position of the target.

At each cycle, the the seekers take measurements and store the samples for later use in plotting the results.

Import required packages:

>>> import c4dynamics as c4d
>>> from matplotlib import pyplot as plt
>>> import numpy as np

Settings and initial conditions:

>>> dt = 0.01
>>> np.random.seed(321)
>>> tgt = c4d.datapoint(x = 1000, vx = -80 * c4d.kmh2ms, vy = 10 * c4d.kmh2ms)
>>> pedestal = c4d.rigidbody(z = 30, theta = -1 * c4d.d2r)
>>> skr = c4d.sensors.seeker(origin = pedestal, dt = 0.05)
>>> skr_ideal = c4d.sensors.seeker(origin = pedestal, isideal = True)

Main loop:

>>> for t in np.arange(0, 60, dt):
...   tgt.inteqm(np.zeros(3), dt)   
...   skr_ideal.measure(tgt, t = t, store = True)     
...   skr.measure(tgt, t = t, store = True)     
...   tgt.store(t)

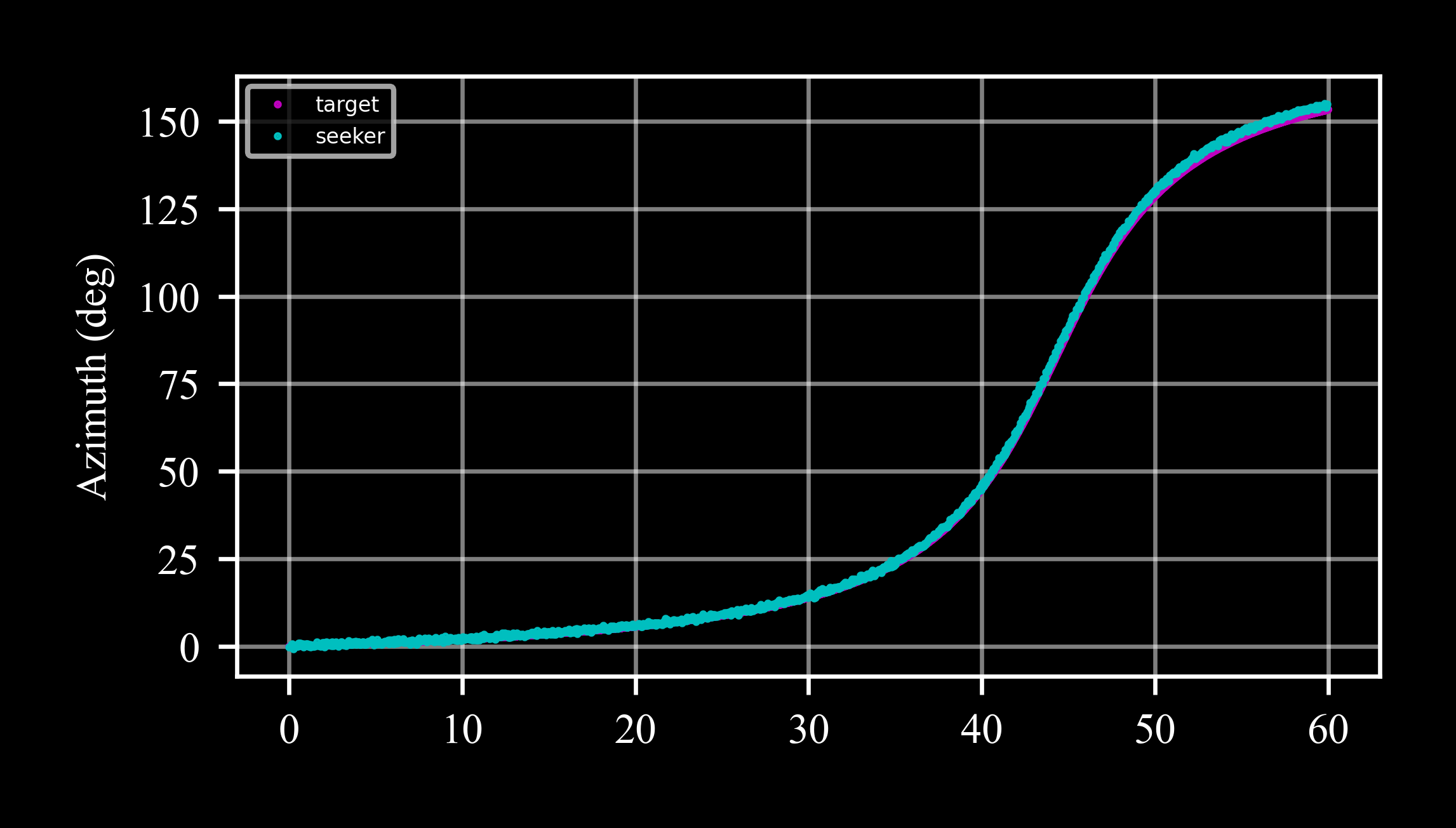
Before viewing the results, let’s examine the error parameters generated by the errors model (c4d.r2d converts radians to degrees):

>>> skr.bias * c4d.r2d 
0.16...
>>> skr.scale_factor 
1.008...
>>> skr.noise_std * c4d.r2d
0.4

Then we excpect a constant bias of -0.02° and a ‘compression’ or ‘squeeze’ of 5% with respect to the target (as represented by the ideal seeker):

>>> ax = plt.subplot()   
>>> ax.plot(*skr_ideal.data('az', scale = c4d.r2d), '.m', markersize = 1, label = 'target')   
>>> ax.plot(*skr.data('az', scale = c4d.r2d), '.c', markersize = 1, label = 'seeker')   

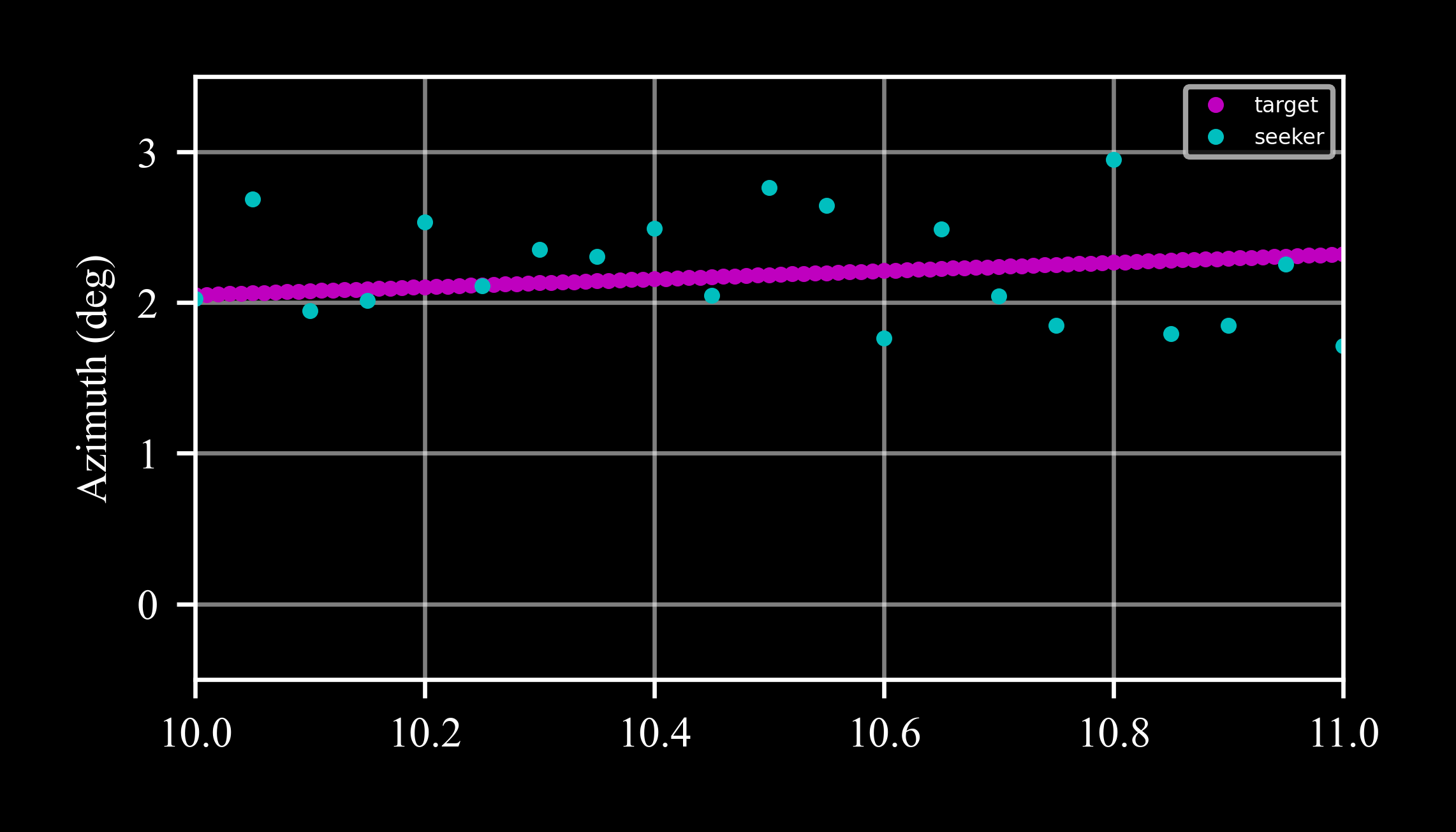
The sample rate of the seeker was set by the parameter dt = 0.05. In cycles that don’t satisfy t < last_t + dt, measure returns None, as shown in a close-up view: