c4dynamics.eqm.integrate.int3

c4dynamics.eqm.integrate.int3(dp: datapoint, forces: ndarray | list, dt: float, derivs_out: bool = False) → ndarray[Any, dtype[float64]] | Tuple[ndarray[Any, dtype[float64]], ndarray[Any, dtype[float64]]]

A step integration of the equations of translational motion.

This method makes a numerical integration using the fourth-order Runge-Kutta method.

The integrated derivatives are of three dimensional translational motion as given by eqm3.

The result is an integrated state in a single interval of time where the size of the step is determined by the parameter dt.

Parameters:

• dp (datapoint) – The datapoint which state vector is to be integrated.

• forces (numpy.array or list) – An external forces array acting on the body.

• dt (float) – Time step for integration.

• derivs_out (bool, optional) – If true, returns the last three derivatives as an estimation for the acceleration of the datapoint.

Returns:

• X (numpy.float64) – An integrated state.

• dxdt4 (numpy.float64, optional) – The last three derivatives of the equations of motion. These derivatives can use as an estimation for the acceleration of the datapoint. Returned if derivs_out is set to True.

Algorithm

The integration steps follow the Runge-Kutta method:

1. Compute k1 = f(ti, yi)

2. Compute k2 = f(ti + dt / 2, yi + dt * k1 / 2)

3. Compute k3 = f(ti + dt / 2, yi + dt * k2 / 2)

4. Compute k4 = f(ti + dt, yi + dt * k3)

5. Update yi = yi + dt / 6 * (k1 + 2 * k2 + 2 * k3 + k4)

Examples

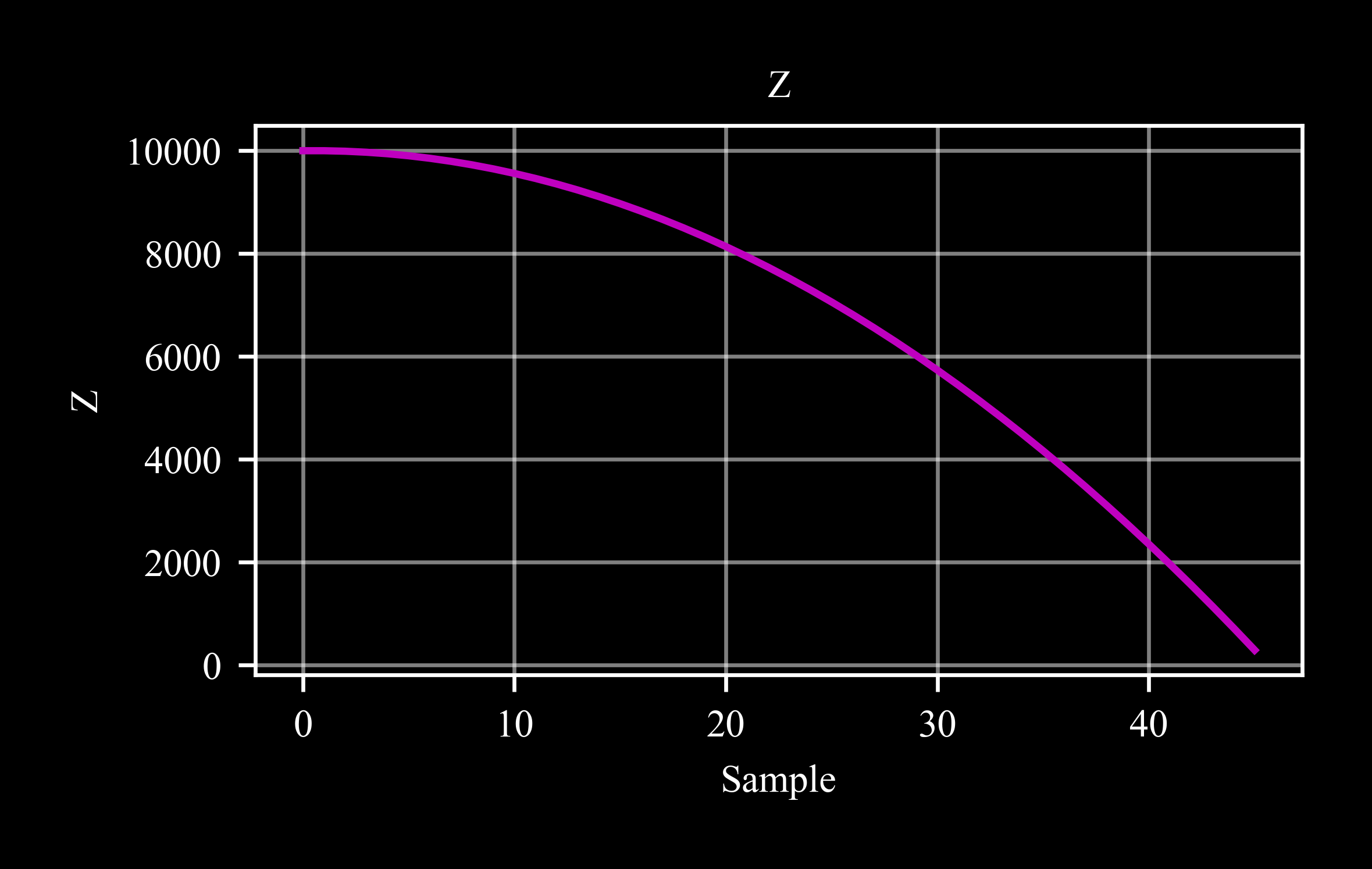
Runge-Kutta integration of the equations of motion on a mass in a free fall (compare to the same example in eqm3 with Euler integration):

Import required packages

>>> import c4dynamics as c4d

>>> pt = c4d.datapoint(z = 10000)
>>> while pt.z > 0:
...   pt.store()
...   pt.X = c4d.eqm.int3(pt, [0, 0, -c4d.g_ms2], dt = 1)