c4dynamics.states.lib.datapoint.datapoint.plot

datapoint.plot(var, scale=1, ax=None, filename=None, darkmode=True, **kwargs)

Draws plots of trajectories or variable evolution over time.

var can be each one of the state variables, or top, side, for trajectories.

Parameters:

• var (str) – The variable to be plotted. Possible variables for trajectories: top, side. For time evolution, any one of the state variables is possible: x, y, z, vx, vy, vz - for a datapoint object, and also phi, theta, psi, p, q, r - for a rigidbody object.

• scale (float or int, optional) – A scaling factor to apply to the variable values. Defaults to 1.

• ax (matplotlib.axes.Axes, optional) – An existing Matplotlib axis to plot on. If None, a new figure and axis will be created. By default None.

• filename (str, optional) – Full file name to save the plot image. If None, the plot will not be saved, by default None.

• darkmode (bool, optional) – Directory path to save the plot image. If None, the plot will not be saved, by default None.

• **kwargs (dict, optional) – Additional key-value arguments passed to matplotlib.pyplot.plot. These can include any keyword arguments accepted by plot, such as color, linestyle, marker, etc.

Notes

• The method overrides the plot of the parent state object and is applicable to datapoint and its subclass rigidbody.

• Uses matplotlib for plotting.

• Trajectory views (top and side) show the crossrange vs downrange or downrange vs altitude.

Examples

Import necessary packages:

>>> import c4dynamics as c4d
>>> from matplotlib import pyplot as plt
>>> import numpy as np
>>> import scipy

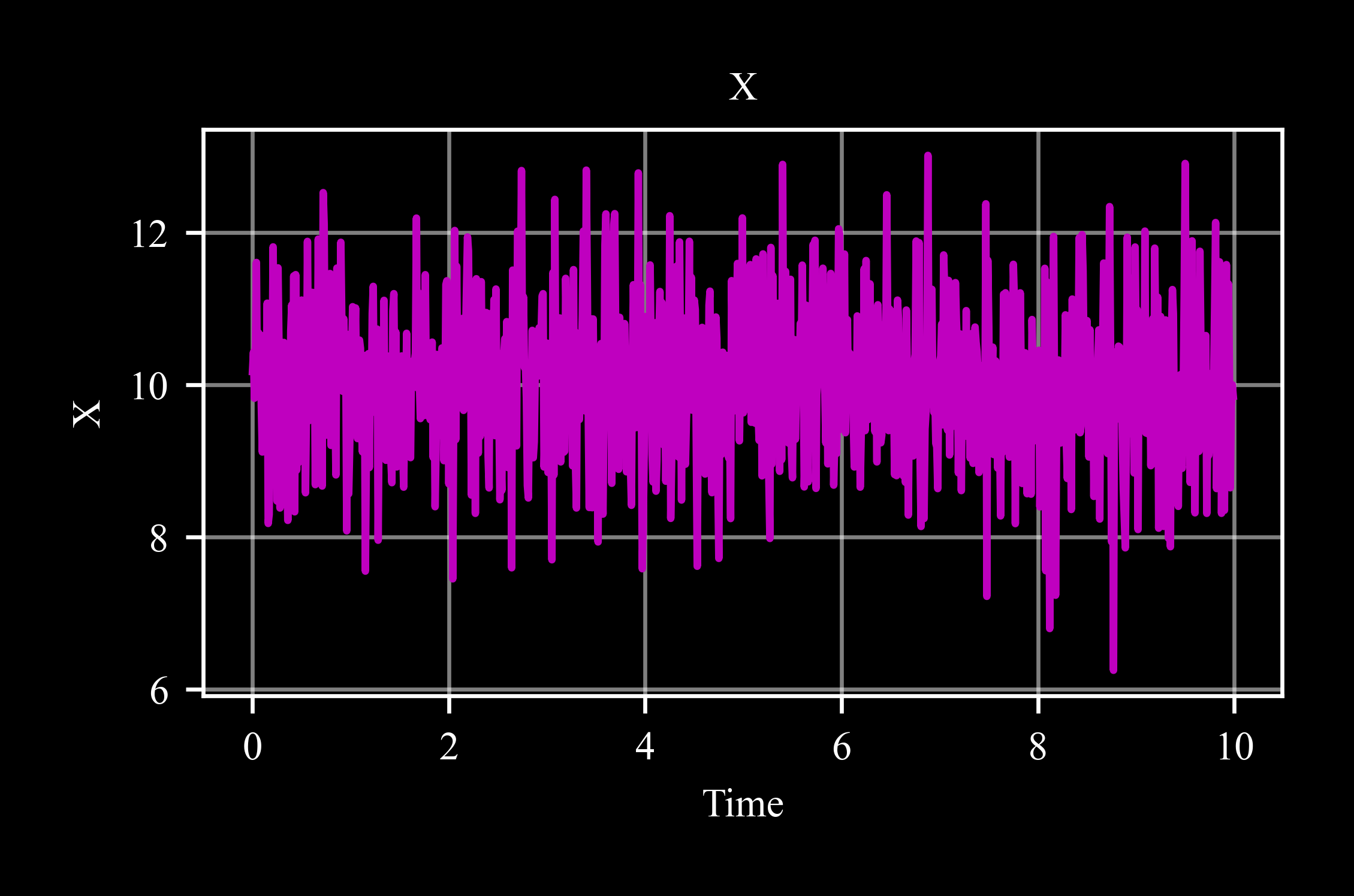
1. datapoint:

>>> pt = c4d.datapoint()
>>> for t in np.arange(0, 10, .01):
...   pt.x = 10 + np.random.randn()
...   pt.store(t)
>>> pt.plot('x')

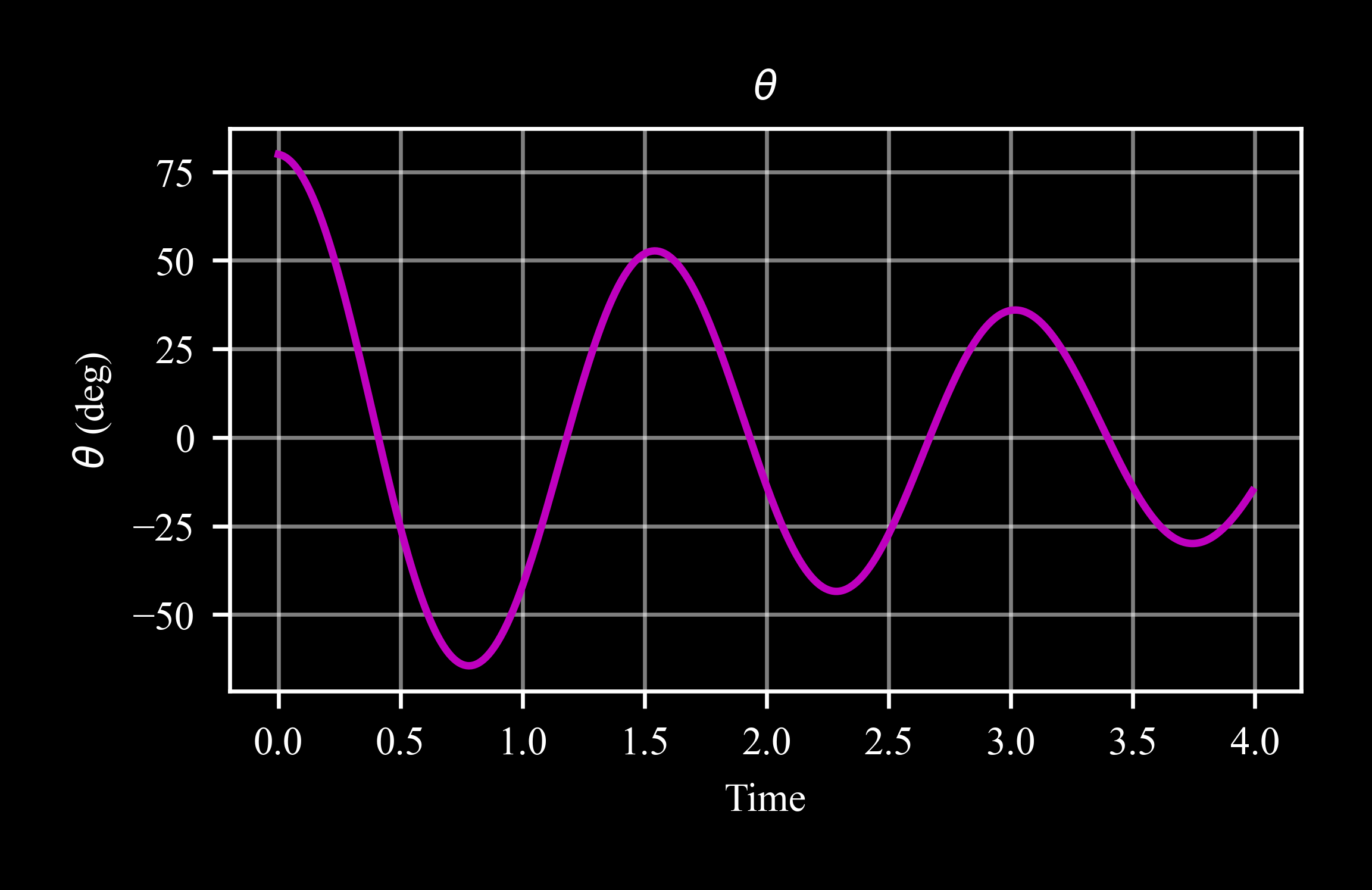
2. rigidbody:

A physical pendulum is represented by a rigidoby object. scipy’s odeint integrates the equations of motion to simulate the angle of rotation of the pendulum over time.

Settings and initial conditions:

>>> dt =.01
>>> pndlm  = c4d.rigidbody(theta = 80 * c4d.d2r)
>>> pndlm.I = [0, .5, 0]

Dynamic equations:

>>> def pendulum(yin, t, Iyy):
...   yout = np.zeros(12)
...   yout[7]  =  yin[10]
...   yout[10] = -c4d.g_ms2 * c4d.sin(yin[7]) / Iyy - .5 * yin[10]
...   return yout

Main loop:

>>> for ti in np.arange(0, 4, dt):
...   pndlm.X = scipy.integrate.odeint(pendulum, pndlm.X, [ti, ti + dt], (pndlm.I[1],))[1]
...   pndlm.store(ti)

Plot results:

>>> pndlm.plot('theta', scale = c4d.r2d)